how to find the parametric equation of a line

Further Applications of Trigonometry

Parametric Equations

Learning Objectives

In this section, you volition:

Parameterize a curve.
Eliminate the parameter.
Find a rectangular equation for a curve defined parametrically.
Notice parametric equations for curves defined by rectangular equations.

Consider the path a moon follows equally it orbits a planet, which simultaneously rotates around the sun, as seen in (Figure). At any moment, the moon is located at a particular spot relative to the planet. But how practise we write and solve the equation for the position of the moon when the distance from the planet, the speed of the moon's orbit around the planet, and the speed of rotation effectually the sun are all unknowns? We tin solve just for one variable at a time.

Illustration of a planet's circular orbit around the sun. — **Figure 1.**

In this section, we will consider sets of equations given past $\,x\left(t\right)\,$ and $\,y\left(t\right)\,$ where $t$ is the independent variable of fourth dimension. Nosotros can utilize these parametric equations in a number of applications when nosotros are looking for not simply a particular position but also the direction of the movement. As nosotros trace out successive values of $\,t,\,$ the orientation of the bend becomes clear. This is one of the primary advantages of using parametric equations: nosotros are able to trace the move of an object along a path according to time. Nosotros begin this department with a await at the basic components of parametric equations and what it means to parameterize a curve. Then we volition acquire how to eliminate the parameter, translate the equations of a curve defined parametrically into rectangular equations, and find the parametric equations for curves defined by rectangular equations.

Parameterizing a Bend

When an object moves along a curve—or curvilinear path—in a given direction and in a given amount of fourth dimension, the position of the object in the plane is given by the x-coordinate and the y-coordinate. Still, both $\,x\,$ and $\,y\,$
vary over time and and so are functions of time. For this reason, we add some other variable, the parameter, upon which both $\,x\,$ and $\,y\,$ are dependent functions. In the example in the section opener, the parameter is time, $\,t.\,$ The $\,x\,$ position of the moon at time, $\,t,\,$ is represented as the function $\,x\left(t\right),\,$ and the $\,y\,$ position of the moon at time, $\,t,\,$ is represented as the part $\,y\left(t\right).\,$ Together, $\,x\left(t\right)\,$ and $\,y\left(t\right)\,$ are called parametric equations, and generate an ordered pair $\,\left(x\left(t\right),\,y\left(t\right)\right).\,$ Parametric equations primarily describe movement and direction.

When we parameterize a curve, nosotros are translating a single equation in two variables, such every bit $\,x\,$ and $\,y ,$ into an equivalent pair of equations in three variables, $\,x,y,\,$ and $\,t.\,$ One of the reasons we parameterize a bend is because the parametric equations yield more than information: specifically, the direction of the object's motion over time.

When we graph parametric equations, nosotros tin observe the individual behaviors of $\,x\,$ and of $\,y.\,$ There are a number of shapes that cannot exist represented in the grade $\,y=f\left(x\right),\,$ meaning that they are not functions. For case, consider the graph of a circle, given equally $\,{r}^{2}={x}^{2}+{y}^{2}.\,$ Solving for $\,y\,$ gives $\,y=±\sqrt{{r}^{2}-{x}^{2}},\,$ or ii equations: $\,{y}_{1}=\sqrt{{r}^{2}-{x}^{2}}\,$ and $\,{y}_{2}=-\sqrt{{r}^{2}-{x}^{2}}.\,$ If nosotros graph $\,{y}_{1}\,$ and $\,{y}_{2}\,$ together, the graph will not pass the vertical line test, as shown in (Figure). Thus, the equation for the graph of a circumvolve is not a function.

Graph of a circle in the rectangular coordinate system - the vertical line test shows that the circle r^2 = x^2 + y^2 is not a function. The dotted red vertical line intersects the function in two places - it should only intersect in one place to be a function. — **Figure two.**

Nevertheless, if we were to graph each equation on its own, each one would pass the vertical line test and therefore would represent a office. In some instances, the concept of breaking up the equation for a circle into two functions is like to the concept of creating parametric equations, equally we apply two functions to produce a non-role. This will go clearer every bit we move frontwards.

Parameterizing a Curve

Parameterize the bend $\,y={x}^{2}-1\,$ letting $\,x\left(t\right)=t.\,$ Graph both equations.

Analysis

The arrows indicate the direction in which the curve is generated. Observe the curve is identical to the bend of $\,y={x}^{2}-1.$

Try It

Construct a table of values and plot the parametric equations: $\,x\left(t\right)=t-3,\,\,y\left(t\right)=2t+4;\,\,\,-1\le t\le 2.$

Finding a Pair of Parametric Equations

Find a pair of parametric equations that models the graph of $\,y=1-{x}^{2},\,$ using the parameter $\,x\left(t\right)=t.\,$ Plot some points and sketch the graph.

Try Information technology

Parameterize the curve given past $\,x={y}^{3}-2y.$

[reveal-answer q="fs-id1165137843239″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165137843239″]
$\begin{array}{l}x\left(t\right)={t}^{3}-2t\\ y\left(t\right)=t\end{array}$ [/hidden-answer]

Finding Parametric Equations That Model Given Criteria

An object travels at a steady rate forth a straight path $\,\left(-5,\,3\right)\,$ to $\,\left(3,\,-1\right)\,$ in the same plane in iv seconds. The coordinates are measured in meters. Discover parametric equations for the position of the object.

[reveal-answer q="fs-id1165137563061″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137563061″]

The parametric equations are simple linear expressions, but we need to view this problem in a step-by-step fashion. The 10-value of the object starts at $\,-5\,$ meters and goes to iii meters. This means the distance 10 has inverse by 8 meters in four seconds, which is a rate of $\,\frac{\text{8 m}}{4\text{ s}},$ or $\,2\,\text{m}/\text{s}.\,$ Nosotros can write the ten-coordinate as a linear function with respect to time as $\,x\left(t\right)=2t-5.\,$ In the linear function template $\,y=mx+b,2t=mx\,$ and $\,-5=b.$

Similarly, the y-value of the object starts at 3 and goes to $\,-1,\,$ which is a change in the distance y of −iv meters in 4 seconds, which is a rate of $\,\frac{-4\text{ m}}{4\text{ s}},$ or $\,-1\text{m}/\text{s}.\,$ We can also write the y-coordinate as the linear function $\,y\left(t\right)=-t+3.\,$ Together, these are the parametric equations for the position of the object, where $\,x\,$
and $\,y\,$
are expressed in meters and $\,t\,$
represents time:

$\begin{array}{l}x\left(t\right)=2t-5\hfill \\ y\left(t\right)=-t+3\hfill \end{array}$

Using these equations, nosotros can build a table of values for $\,t,x,\,$ and $\,y$ (see (Figure)). In this example, we limited values of $\,t\,$ to non-negative numbers. In general, whatsoever value of $\,t\,$ tin be used.

$t$	$x\left(t\right)=2t-5$	$y\left(t\right)=-t+3$
$0$	$x=2\left(0\right)-5=-5$	$y=-\left(0\right)+3=3$
$1$	$x=2\left(1\right)-5=-3$	$y=-\left(1\right)+3=2$
$2$	$x=2\left(2\right)-5=-1$	$y=-\left(2\right)+3=1$
$3$	$x=2\left(3\right)-5=1$	$y=-\left(3\right)+3=0$
$4$	$x=2\left(4\right)-5=3$	$y=-\left(4\right)+3=-1$

From this tabular array, nosotros can create 3 graphs, as shown in (Figure).

Analysis

Again, nosotros see that, in (Effigy)(c), when the parameter represents time, we can signal the movement of the object forth the path with arrows.

Eliminating the Parameter

In many cases, nosotros may have a pair of parametric equations but notice that it is simpler to draw a curve if the equation involves only two variables, such as $\,x\,$ and $\,y.\,$ Eliminating the parameter is a method that may make graphing some curves easier. Withal, if we are concerned with the mapping of the equation co-ordinate to time, and so it will be necessary to betoken the orientation of the curve equally well. There are diverse methods for eliminating the parameter $\,t\,$ from a ready of parametric equations; not every method works for every type of equation. Here nosotros volition review the methods for the most common types of equations.

Eliminating the Parameter from Polynomial, Exponential, and Logarithmic Equations

For polynomial, exponential, or logarithmic equations expressed every bit two parametric equations, we cull the equation that is most easily manipulated and solve for $\,t.\,$ We substitute the resulting expression for $\,t\,$
into the 2nd equation. This gives one equation in $\,x\,$ and $\,y.\,$

Eliminating the Parameter in Polynomials

Given $\,x\left(t\right)={t}^{2}+1\,$ and $\,y\left(t\right)=2+t,\,$ eliminate the parameter, and write the parametric equations every bit a Cartesian equation.

[reveal-answer q="fs-id1165135250612″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165135250612″]

We will begin with the equation for $\,y\,$ because the linear equation is easier to solve for $\,t.$

$\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=2+t\hfill \\ y-2=t\hfill \end{array}$

Next, substitute $\,y-2\,$ for $\,t\,$ in $\,x\left(t\right).$

$\begin{array}{ll}x={t}^{2}+1\hfill & \hfill \\ x={\left(y-2\right)}^{2}+1\hfill & \text{Substitute the expression for }t\text{ into }x.\hfill \\ x={y}^{2}-4y+4+1\hfill & \hfill \\ x={y}^{2}-4y+5\hfill & \hfill \\ x={y}^{2}-4y+5\hfill & \hfill \end{array}$

The Cartesian course is $\,x={y}^{2}-4y+5.$ [/hidden-answer]

Try It

Given the equations below, eliminate the parameter and write equally a rectangular equation for $\,y\,$ as a function

$\begin{array}{l}\\ \begin{array}{l}x\left(t\right)=2{t}^{2}+6\hfill \\ y\left(t\right)=5-t\hfill \end{array}\end{array}$

[reveal-answer q="fs-id1165133001900″]Show Solution[/reveal-respond]
[hidden-reply a="fs-id1165133001900″]

$y=5-\sqrt{\frac{1}{2}x-3}$

[/subconscious-answer]

Eliminating the Parameter in Exponential Equations

Eliminate the parameter and write as a Cartesian equation: $\,x\left(t\right)={e}^{-t}\,$ and $\,y\left(t\right)=3{e}^{t},\,\,t>0.\,$

[reveal-respond q="fs-id1165137419904″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165137419904″]

Isolate $\,{e}^{t}.\,$

$\begin{array}{l}\,\,x={e}^{-t}\hfill \\ {e}^{t}=\frac{1}{x}\hfill \end{array}$

Substitute the expression into $\,y\left(t\right).$

$\begin{array}{l}y=3{e}^{t}\hfill \\ y=3\left(\frac{1}{x}\right)\hfill \\ y=\frac{3}{x}\hfill \end{array}$

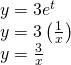
The Cartesian course is $\,y=\frac{3}{x}.$ [/hidden-answer]

Eliminating the Parameter in Logarithmic Equations

Eliminate the parameter and write as a Cartesian equation: $\,x\left(t\right)=\sqrt{t}+2\,$ and $\,y\left(t\right)=\mathrm{log}\left(t\right).$

[reveal-answer q="fs-id1165137482606″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137482606″]

Solve the first equation for $\,t.$

$\begin{array}{ll}\text{ }x=\sqrt{t}+2\hfill & \hfill \\ \text{ }x-2=\sqrt{t}\hfill & \hfill \\ {\left(x-2\right)}^{2}=t\hfill & \text{Square both sides}.\hfill \end{array}$

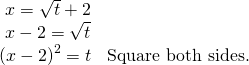
And then, substitute the expression for $t$ into the $y$ equation.

$\begin{array}{l}y=\mathrm{log}\left(t\right)\\ y=\mathrm{log}{\left(x-2\right)}^{2}\end{array}$

The Cartesian form is $\,y=\mathrm{log}{\left(x-2\right)}^{2}.$ [/hidden-answer]

Try It

Eliminate the parameter and write as a rectangular equation.

$\begin{array}{l}\\ \begin{array}{l}x\left(t\right)={t}^{2}\hfill \\ y\left(t\right)=\mathrm{ln}\,t\,\,\,\,\,\,\,\,t>0\hfill \end{array}\end{array}$

[reveal-answer q="fs-id1165137408218″]Show Solution[/reveal-reply]
[hidden-reply a="fs-id1165137408218″]

$y=\mathrm{ln}\sqrt{x}$

[/hidden-answer]

Eliminating the Parameter from Trigonometric Equations

Eliminating the parameter from trigonometric equations is a straightforward commutation. We tin use a few of the familiar trigonometric identities and the Pythagorean Theorem.

Start, we employ the identities:

$\begin{array}{l}x\left(t\right)=a\mathrm{cos}\,t\\ y\left(t\right)=b\mathrm{sin}\,t\end{array}$

Solving for $\,\mathrm{cos}\,t\,$ and $\,\mathrm{sin}\,t,\,$ we have

$\begin{array}{l}\frac{x}{a}=\mathrm{cos}\,t\\ \frac{y}{b}=\mathrm{sin}\,t\end{array}$

Then, use the Pythagorean Theorem:

${\mathrm{cos}}^{2}t+{\mathrm{sin}}^{2}t=1$

Substituting gives

${\mathrm{cos}}^{2}t+{\mathrm{sin}}^{2}t={\left(\frac{x}{a}\right)}^{2}+{\left(\frac{y}{b}\right)}^{2}=1$

Eliminating the Parameter from a Pair of Trigonometric Parametric Equations

Eliminate the parameter from the given pair of trigonometric equations where $\,0\le t\le 2\pi \,$ and sketch the graph.

$\begin{array}{l}x\left(t\right)=4\mathrm{cos}\,t\\ y\left(t\right)=3\mathrm{sin}\,t\end{array}$

[reveal-answer q="fs-id1165135198527″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165135198527″]

Solving for $\,\mathrm{cos}\,t\,$ and $\,\mathrm{sin}\,t,$ nosotros have

$\begin{array}{l}\,x=4\mathrm{cos}\,t\hfill \\ \frac{x}{4}=\mathrm{cos}\,t\hfill \\ \,y=3\mathrm{sin}\,t\hfill \\ \frac{y}{3}=\mathrm{sin}\,t\hfill \end{array}$

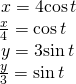
Side by side, utilise the Pythagorean identity and make the substitutions.

$\begin{array}{r}\hfill {\mathrm{cos}}^{2}t+{\mathrm{sin}}^{2}t=1\\ \hfill {\left(\frac{x}{4}\right)}^{2}+{\left(\frac{y}{3}\right)}^{2}=1\\ \hfill \frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1\end{array}$

Graph of given ellipse centered at (0,0). — **Effigy 8.**

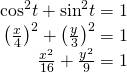
The graph for the equation is shown in (Figure).[/subconscious-answer]

Try It

Eliminate the parameter from the given pair of parametric equations and write every bit a Cartesian equation: $\,x\left(t\right)=2\mathrm{cos}\,t\,$ and $\,y\left(t\right)=3\mathrm{sin}\,t.$

[reveal-answer q="fs-id1165137456226″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165137456226″]

$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1$

[/hidden-answer]

Finding Cartesian Equations from Curves Defined Parametrically

When we are given a set of parametric equations and demand to find an equivalent Cartesian equation, we are essentially "eliminating the parameter." However, at that place are diverse methods we can apply to rewrite a set of parametric equations as a Cartesian equation. The simplest method is to set one equation equal to the parameter, such as $\,x\left(t\right)=t.\,$ In this instance, $\,y\left(t\right)\,$ can be whatsoever expression. For case, consider the post-obit pair of equations.

$\begin{array}{l}x\left(t\right)=t\\ y\left(t\right)={t}^{2}-3\end{array}$

Rewriting this gear up of parametric equations is a affair of substituting $\,x\,$ for $\,t.\,$ Thus, the Cartesian equation is $\,y={x}^{2}-3.$

Finding a Cartesian Equation Using Alternate Methods

Use two different methods to find the Cartesian equation equivalent to the given set of parametric equations.

$\begin{array}{l}\\ \begin{array}{l}x\left(t\right)=3t-2\hfill \\ y\left(t\right)=t+1\hfill \end{array}\end{array}$

[reveal-respond q="fs-id1165135390989″]Bear witness Solution[/reveal-reply]
[hidden-answer a="fs-id1165135390989″]

Method 1. Get-go, allow's solve the $\,x\,$ equation for $\,t.\,$ Then we can substitute the issue into the $y$ equation.

$\begin{array}{l}\text{ }x=3t-2\hfill \\ \text{ }x+2=3t\hfill \\ \frac{x+2}{3}=t\hfill \end{array}$

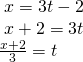
Now substitute the expression for $\,t\,$ into the $\,y\,$ equation.

$\begin{array}{l}y=t+1\hfill \\ y=\left(\frac{x+2}{3}\right)+1\hfill \\ y=\frac{x}{3}+\frac{2}{3}+1\hfill \\ y=\frac{1}{3}x+\frac{5}{3}\hfill \end{array}$

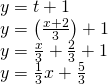
Method two. Solve the $\,y\,$ equation for $\,t\,$ and substitute this expression in the $\,x\,$ equation.

$\begin{array}{l}\text{ }y=t+1\hfill \\ y-1=t\hfill \end{array}$

Make the substitution and and so solve for $\,y.$

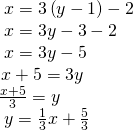$\begin{array}{l}\text{ }x=3\left(y-1\right)-2\hfill \\ \text{ }x=3y-3-2\hfill \\ \text{ }x=3y-5\hfill \\ \,x+5=3y\hfill \\ \frac{x+5}{3}=y\hfill \\ \text{ }y=\frac{1}{3}x+\frac{5}{3}\hfill \end{array}$ [/hidden-respond]

Try It

Write the given parametric equations as a Cartesian equation: $\,x\left(t\right)={t}^{3}\,$ and $\,y\left(t\right)={t}^{6}.$

[reveal-reply q="fs-id1165137437198″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137437198″]

$y={x}^{2}$

[/hidden-respond]

Finding Parametric Equations for Curves Defined by Rectangular Equations

Although nosotros have but shown that there is just ane way to interpret a set of parametric equations as a rectangular equation, there are multiple ways to interpret a rectangular equation as a set of parametric equations. Any strategy we may use to discover the parametric equations is valid if it produces equivalency. In other words, if we choose an expression to represent $\,x,\,$ and then substitute information technology into the $\,y\,$ equation, and it produces the same graph over the same domain as the rectangular equation, so the gear up of parametric equations is valid. If the domain becomes restricted in the set of parametric equations, and the function does not allow the same values for $\,x\,$ equally the domain of the rectangular equation, so the graphs will be different.

Finding a Set of Parametric Equations for Curves Divers past Rectangular Equations

Find a set of equivalent parametric equations for $\,y={\left(x+3\right)}^{2}+1.$

[reveal-answer q="fs-id1165135671968″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135671968″]

An obvious selection would be to let $\,x\left(t\right)=t.\,$ Then $\,y\left(t\right)={\left(t+3\right)}^{2}+1.$ But let'southward try something more interesting. What if nosotros let $\,x=t+3?\,$ Then nosotros have

$\begin{array}{l}y={\left(x+3\right)}^{2}+1\hfill \\ y={\left(\left(t+3\right)+3\right)}^{2}+1\hfill \\ y={\left(t+6\right)}^{2}+1\hfill \end{array}$

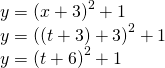
The set of parametric equations is

$\begin{array}{l}\hfill \\ x\left(t\right)=t+3\hfill \\ y\left(t\right)={\left(t+6\right)}^{2}+1\hfill \end{array}$

Encounter (Figure).

Graph of parametric and rectangular coordinate versions of the same parabola - they are the same! — **Figure 6.**

[/hidden-answer]

Fundamental Concepts

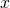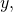Parameterizing a bend involves translating a rectangular equation in two variables, $\,x\,$ and $\,y,\,$ into two equations in three variables, 10, y, and t. Often, more than information is obtained from a prepare of parametric equations. See (Figure), (Figure), and (Effigy).
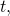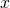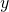Sometimes equations are simpler to graph when written in rectangular form. Past eliminating $\,t,\,$ an equation in $\,x\,$ and $\,y\,$ is the result.
To eliminate 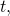$\,t,\,$ solve one of the equations for 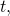$\,t,\,$ and substitute the expression into the second equation. Encounter (Effigy), (Effigy), (Effigy), and (Figure).
Finding the rectangular equation for a curve defined parametrically is basically the same as eliminating the parameter. Solve for 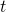$\,t\,$ in one of the equations, and substitute the expression into the second equation. Meet (Figure).
There are an space number of means to choose a set of parametric equations for a bend divers as a rectangular equation.
Discover an expression for 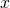$\,x\,$ such that the domain of the set of parametric equations remains the aforementioned as the original rectangular equation. See (Figure).

Section Exercises

Verbal

What is a organization of parametric equations?

[reveal-answer q="fs-id1165135457745″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1165135457745″]

A pair of functions that is dependent on an external gene. The two functions are written in terms of the same parameter. For example, $\,x=f\left(t\right)\,$ and $\,y=f\left(t\right).$

[/hidden-answer]

Some examples of a 3rd parameter are time, length, speed, and scale. Explicate when time is used as a parameter.

Explain how to eliminate a parameter given a set of parametric equations.

[reveal-answer q="fs-id1165137768026″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1165137768026″]

Choose one equation to solve for $\,t,\,$ substitute into the other equation and simplify.

[/hidden-reply]

What is a benefit of writing a organisation of parametric equations as a Cartesian equation?

What is a benefit of using parametric equations?

[reveal-respond q="fs-id1165135250841″]Bear witness Solution[/reveal-reply]
[hidden-answer a="fs-id1165135250841″]

Some equations cannot be written as functions, like a circumvolve. Even so, when written as ii parametric equations, separately the equations are functions.

[/hidden-answer]

Why are in that location many sets of parametric equations to represent on Cartesian part?

Algebraic

For the following exercises, eliminate the parameter $\,t\,$ to rewrite the parametric equation as a Cartesian equation.

$\{\begin{array}{l}x(t)=5-t\hfill \\ y(t)=8-2t\hfill \end{array}$

[reveal-answer q="fs-id1165135389966″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165135389966″]

$y=-2+2x$

[/subconscious-answer]

$\{\begin{array}{l}x(t)=6-3t\hfill \\ y(t)=10-t\hfill \end{array}$

$\{\begin{array}{l}x(t)=2t+1\hfill \\ y(t)=3\sqrt{t}\hfill \end{array}$

[reveal-answer q="fs-id1165137463947″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165137463947″]

$y=3\sqrt{\frac{x-1}{2}}$

[/hidden-respond]

$\{\begin{array}{l}x(t)=3t-1\hfill \\ y(t)=2{t}^{2}\hfill \end{array}$

$\{\begin{array}{l}x(t)=2{e}^{t}\hfill \\ y(t)=1-5t\hfill \end{array}$

[reveal-answer q="fs-id1165135496291″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165135496291″]

$x=2{e}^{\frac{1-y}{5}}\,$ or $\,y=1-5ln\left(\frac{x}{2}\right)$

[/hidden-reply]

$\{\begin{array}{l}x(t)={e}^{-2t}\hfill \\ y(t)=2{e}^{-t}\hfill \end{array}$

$\{\begin{array}{l}x(t)=4\text{log}(t)\hfill \\ y(t)=3+2t\hfill \end{array}$

[reveal-answer q="fs-id1165135353727″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165135353727″]

$x=4\mathrm{log}\left(\frac{y-3}{2}\right)$

[/hidden-answer]

$\{\begin{array}{l}x(t)=\text{log}(2t)\hfill \\ y(t)=\sqrt{t-1}\hfill \end{array}$

$\{\begin{array}{l}x(t)={t}^{3}-t\hfill \\ y(t)=2t\hfill \end{array}$

[reveal-answer q="fs-id1165137803762″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137803762″]

$x={\left(\frac{y}{2}\right)}^{3}-\frac{y}{2}$

[/hidden-answer]

$\{\begin{array}{l}x(t)=t-{t}^{4}\hfill \\ y(t)=t+2\hfill \end{array}$

$\{\begin{array}{l}x(t)={e}^{2t}\hfill \\ y(t)={e}^{6t}\hfill \end{array}$

[reveal-respond q="fs-id1165135414214″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135414214″]

$y={x}^{3}$

[/hidden-answer]

$\{\begin{array}{l}x(t)={t}^{5}\hfill \\ y(t)={t}^{10}\hfill \end{array}$

$\{\begin{array}{l}x(t)=4\text{cos}\,t\hfill \\ y(t)=5\mathrm{sin}\,t \hfill \end{array}$

[reveal-respond q="fs-id1165137762341″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1165137762341″]

${\left(\frac{x}{4}\right)}^{2}+{\left(\frac{y}{5}\right)}^{2}=1$

[/hidden-answer]

$\{\begin{array}{l}x(t)=3\mathrm{sin}\,t\hfill \\ y(t)=6\mathrm{cos}\,t\hfill \end{array}$

$\{\begin{array}{l}x(t)=2{\text{cos}}^{2}t\hfill \\ y(t)=-\mathrm{sin}\,t \hfill \end{array}$

[reveal-answer q="fs-id1165137602808″]Testify Solution[/reveal-reply]
[hidden-answer a="fs-id1165137602808″]
${y}^{2}=1-\frac{1}{2}x$ [/hidden-answer]

$\{\begin{array}{l}x(t)=\mathrm{cos}\,t+4\\ y(t)=2{\mathrm{sin}}^{2}t\end{array}$

$\{\begin{array}{l}x(t)=t-1\\ y(t)={t}^{2}\end{array}$

[reveal-answer q="fs-id1165133213863″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165133213863″]

$y={x}^{2}+2x+1$

[/hidden-respond]

$\{\begin{array}{l}x(t)=-t\\ y(t)={t}^{3}+1\end{array}$

$\{\begin{array}{l}x(t)=2t-1\\ y(t)={t}^{3}-2\end{array}$

[reveal-answer q="fs-id1165137704906″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165137704906″]

$y={\left(\frac{x+1}{2}\right)}^{3}-2$

[/subconscious-answer]

For the post-obit exercises, rewrite the parametric equation as a Cartesian equation by building an $x\text{-}y$ table.

$\{\begin{array}{l}x(t)=2t-1\\ y(t)=t+4\end{array}$

$\{\begin{array}{l}x(t)=4-t\\ y(t)=3t+2\end{array}$

[reveal-answer q="fs-id1165134495094″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165134495094″]

$y=-3x+14$

[/hidden-answer]

$\{\begin{array}{l}x(t)=2t-1\\ y(t)=5t\end{array}$

$\{\begin{array}{l}x(t)=4t-1\\ y(t)=4t+2\end{array}$

[reveal-answer q="fs-id1165134187207″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165134187207″]

$y=x+3$

[/hidden-answer]

For the following exercises, parameterize (write parametric equations for) each Cartesian equation by setting $x\left(t\right)=t$ or by setting $\,y\left(t\right)=t.$

$y\left(x\right)=3{x}^{2}+3$

$y\left(x\right)=2\mathrm{sin}\,x+1$

[reveal-answer q="fs-id1165137925225″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137925225″]

$\{\begin{array}{l}x(t)=t\hfill \\ y(t)=2\mathrm{sin}t+1\hfill \end{array}$

[/hidden-answer]

$x\left(y\right)=3\mathrm{log}\left(y\right)+y$

$x\left(y\right)=\sqrt{y}+2y$

[reveal-reply q="fs-id1165137575928″]Bear witness Solution[/reveal-answer]
[subconscious-answer a="fs-id1165137575928″]

$\{\begin{array}{l}x(t)=\sqrt{t}+2t\hfill \\ y(t)=t\hfill \end{array}$

[/subconscious-answer]

For the following exercises, parameterize (write parametric equations for) each Cartesian equation by using $x\left(t\right)=a\mathrm{cos}\,t$ and $\,y\left(t\right)=b\mathrm{sin}\,t.\,$ Identify the curve.

$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}=1$

$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{36}=1$

[reveal-answer q="fs-id1165137849389″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165137849389″]

$\{\begin{array}{l}x(t)=4\mathrm{cos}\,t\hfill \\ y(t)=6\mathrm{sin}\,t\hfill \end{array};\,$ Ellipse

[/subconscious-answer]

${x}^{2}+{y}^{2}=16$

${x}^{2}+{y}^{2}=10$

[reveal-respond q="fs-id1165137559264″]Prove Solution[/reveal-reply]
[hidden-answer a="fs-id1165137559264″]

$\{\begin{array}{l}x(t)=\sqrt{10}\mathrm{cos}t\hfill \\ y(t)=\sqrt{10}\mathrm{sin}t\hfill \end{array};\,$
Circle

[/hidden-reply]

Parameterize the line from $\,\left(-1,0\right)\,$ to $\,\left(3,-2\right)\,$ so that the line is at $\,\left(-1,0\right)\,$ at $\,t=0,\,$ and at $\,\left(3,-2\right)\,$ at $\,t=1.$

[reveal-answer q="fs-id1165137400302″]Show Solution[/reveal-respond]
[subconscious-answer a="fs-id1165137400302″]

$\{\begin{array}{l}x(t)=-1+4t\hfill \\ y(t)=-2t\hfill \end{array}$

[/hidden-answer]

Parameterize the line from $\,\left(4,1\right)\,$ to $\,\left(6,-2\right)\,$ so that the line is at $\,\left(4,1\right)\,$ at $\,t=0,\,$ and at $\,\left(6,-2\right)\,$ at $\,t=1.$

[reveal-answer q="fs-id1165134164960″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165134164960″]

$\{\begin{array}{l}x(t)=4+2t\hfill \\ y(t)=1-3t\hfill \end{array}$

[/hidden-respond]

Technology

For the following exercises, utilise the table feature in the graphing calculator to decide whether the graphs intersect.

$\{\begin{array}{l}{x}_{1}(t)=3t\hfill \\ {y}_{1}(t)=2t-1\hfill \end{array}\text{ and }\{\begin{array}{l}{x}_{2}(t)=t+3\hfill \\ {y}_{2}(t)=4t-4\hfill \end{array}$

$\{\begin{array}{l}{x}_{1}(t)={t}^{2}\hfill \\ {y}_{1}(t)=2t-1\hfill \end{array}\text{ and }\{\begin{array}{l}{x}_{2}(t)=-t+6\hfill \\ {y}_{2}(t)=t+1\hfill \end{array}$

[reveal-answer q="fs-id1165137453625″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165137453625″]

yes, at $t=2$

[/subconscious-reply]

For the following exercises, use a graphing calculator to complete the tabular array of values for each set of parametric equations.

[reveal-answer q="fs-id1165137737862″]Show Solution[/reveal-respond]
[hidden-reply a="fs-id1165137737862″]


$t$	$x$	$y$
1	-iii	1
ii	0	7
3	v	17

[/subconscious-reply]

Extensions

Find 2 different sets of parametric equations for $\,y={\left(x+1\right)}^{2}.$

[reveal-answer q="fs-id1165137437388″]Evidence Solution[/reveal-answer]
[subconscious-reply a="fs-id1165137437388″]

answers may vary: $\,\{\begin{array}{l}x(t)=t-1\hfill \\ y(t)={t}^{2}\hfill \end{array}\text{ and }\{\begin{array}{l}x(t)=t+1\hfill \\ y(t)={(t+2)}^{2}\hfill \end{array}$

[/hidden-answer]

Detect ii different sets of parametric equations for $\,y=3x-2.$

Notice two different sets of parametric equations for $\,y={x}^{2}-4x+4.$

[reveal-answer q="fs-id1165137834340″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1165137834340″]

answers may vary: , $\,\{\begin{array}{l}x(t)=t\hfill \\ y(t)={t}^{2}-4t+4\hfill \end{array}\text{ and }\{\begin{array}{l}x(t)=t+2\hfill \\ y(t)={t}^{2}\hfill \end{array}$

[/hidden-answer]

Source: https://opentextbc.ca/algebratrigonometryopenstax/chapter/parametric-equations/

Posted by: cruzfith1969.blogspot.com

how to find the parametric equation of a line

Parametric Equations

Learning Objectives

Parameterizing a Bend

Parameterizing a Curve

Analysis

Try It

Finding a Pair of Parametric Equations

Try Information technology

Finding Parametric Equations That Model Given Criteria

Analysis

Eliminating the Parameter

Eliminating the Parameter from Polynomial, Exponential, and Logarithmic Equations

Eliminating the Parameter in Polynomials

Try It

Eliminating the Parameter in Exponential Equations

Eliminating the Parameter in Logarithmic Equations

Try It

Eliminating the Parameter from Trigonometric Equations

Eliminating the Parameter from a Pair of Trigonometric Parametric Equations

Try It

Finding Cartesian Equations from Curves Defined Parametrically

Finding a Cartesian Equation Using Alternate Methods

Try It

Finding Parametric Equations for Curves Defined by Rectangular Equations

Finding a Set of Parametric Equations for Curves Divers past Rectangular Equations

Fundamental Concepts

Section Exercises

Verbal

Algebraic

Technology

Extensions

0 Response to "how to find the parametric equation of a line"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel